1. QuantLibを使ってみる
1.2 Example を試す
1.2.7 Gaussian1dModels : Gaussian Short Rate Model と Markov Functional Model
1.2.7.4 ソースコードの解析 (その3)
1.2.7.4.6 Call Option付きの債券の価格評価(364~461行目)
Call Option が付いた債券の価格評価については、すでに CallableBonds プロジェクトでも行いました。そこでは、商品オブジェクトとして、Bond クラスのオブジェクトを作成し、Hull-White Model を使った価格エンジンで価格評価をテストしました。ここでは、Bond クラスではなく、NonStandardSwaption クラスを応用して、Call Option 付債券の価格評価を行っています。CallableBonds プロジェクトと違う点は、
- CallableBonds プロジェクトでは、シンプルな Hull-White Model を使ったので、Volatility の期間構造にフィットできなかったが、 GSR モデルの Volatilityは、時間の関数と看做すので、Volatilityの期間構造によりフィットした形で導出できる。
- CallableBonds プロジェクトでは、forecasting curve と discounting curve で同じカーブを使っていたが、ここでは、両者を分ける multi-curve 方式で価格評価を行う。特に、forecasting curveについては、債券発行体のクレジットスプレッドを勘案したものを使う。
- CalibrationHelperの配列も、CallableBondsプロジェクトでは外生的に与えていましたが、ここではcalibrationBasket()関数を使って自動的に生成する。従って、ストライク金利を債券のクーポンやクレジットスプレッドを勘案した形でCalibrationHelperを生成する事が可能。
以上のような違いに留意しながら、コードの内容を見て行きます。
(1) Call Option付債券の商品オブジェクトの作成(374~382行目)
まずCall Option付債券の商品オブジェクトを、部品から作り上げます。ここでは、Bondクラスのオブジェクトを作るのではなく、NonStandardSwapクラスのオブジェクトとして作成しています。スワップのキャッシュフローの内、変動金利サイドのみなし元本を0にし、固定金利サイドだけを使えば、固定金利債券と全く同じキャッシュフローを作ることができます(374~376行目でそのような設定を行っています)。なので、そのキャッシュフローを債券と看做して、価格やリスク量の計算ができます。さらに、このクラスを使う事で、このクラスに備わっているcalibrationBasket()関数を使う事ができます。378行目にあるコンストラクターと、その引数(部品)を下記します。
auto underlying3 = ext::make_shared<NonstandardSwap>(
Swap::Receiver, :債券のCash Flowを固定金利の受取CFと看做す
nominalFixed2, :債券の元本を固定金利CFのみなし元本とみなす
nominalFloating2, :変動金利CFの看做し元本は375行目で0に設定
fixedSchedule, :固定金利CFのスケジュール
strikes, :Call Option行使の際の償還額
Thirty360(Thirty360::BondBasis), :固定金利CFの日数計算方法
floatingSchedule, :変動金利CFのスケジュール
euribor6m, :変動金利インデックス
1.0, :レバレッジ
0.0, :変動金利スプレッド
Actual360(), :変動金利日数計算方法
false, :途中でのみなし元本交換を"false"なしに設定
true :最終期日でのみなし元本の交換を“true”ありに設定
); (2) (1)のスワップ(債券CF)を対象とする、バーミューダン・スワップションを作成(386行目)
さらに、(1)を対象資産とするバーミューダン・スワップションを作成すれば、Call Option付債券と同じ特性を持ったスワップションが出来上がる。 これをCall Option付き債券と看做す。
auto swaption3 = ext::make_shared<NonstandardSwaption>(
underlying3, :上記で生成した債券に模したスワップ
exercise2 :386行目で生成したリベート付きの行使価格
); (3) 次に、債券のクレジットスプレッドを 0 と 100bp の2通り用意(388,389行目 oas0 と oas100)
これを価格エンジンに与えるとGSRモデルの中心回帰レベルとなる forecasting curve が、Swapカーブ+クレジットスプレッドに修正される(392~394行目)。
(4) CalibrationHelper の自動作成と、Calibration の実行、価格評価-1(396~422行目)
まず、クレジットスプレッドを 0 に設定して、calibrationBasket()関数を呼び、CalibrationHelperを生成する。さらに、calibrateVolatilitiesIterative()関数で、calibrationを実行。最後に NPV を計算。
(5) CalibrationHelper の自動作成と、Calibration の実行、価格評価-2(429~461行目)
次に、クレジットスプレッドを100bpに設定し、calibrationBasket()関数を呼び、CalibrationHelperを生成する。さらに、calibrateVolatilitiesIterative()関数で、calibrationを実行。最後にNPVを計算。
以上の実行結果のConsole画面出力を下記に添付します。
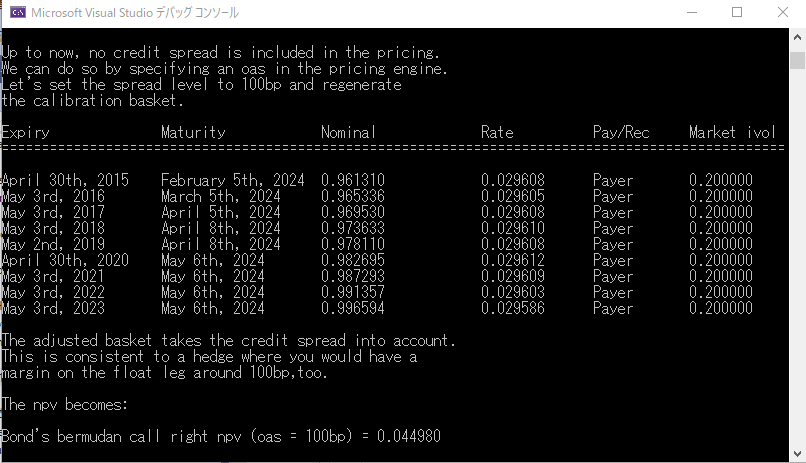
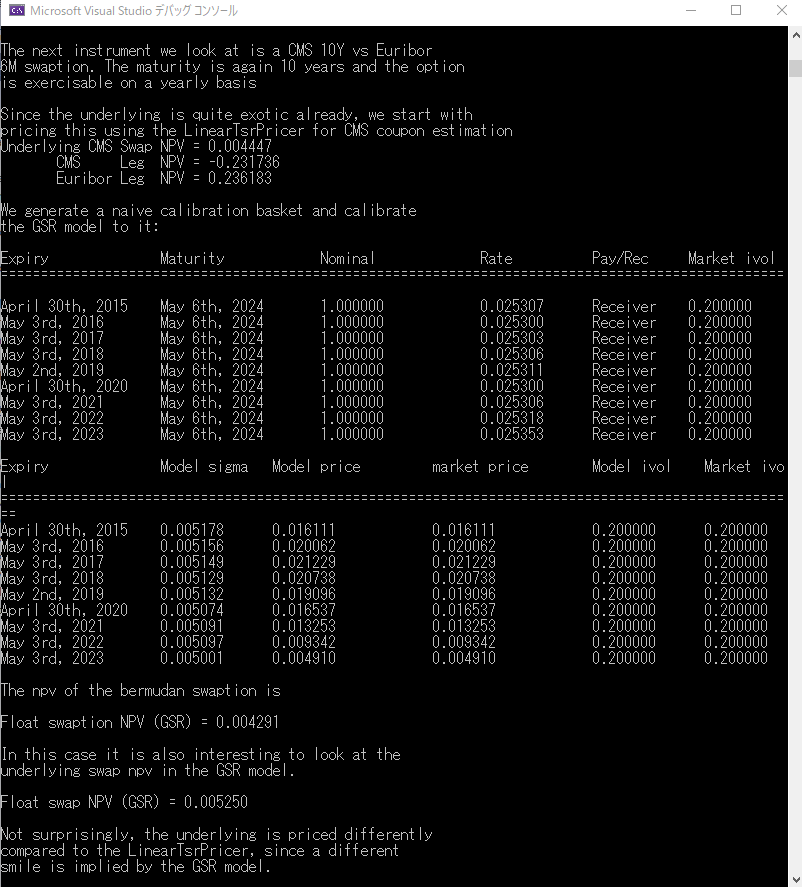
この出力結果の見るべきポイントは、
- oas0 すなわち、クレジットスプレッド=0 のケースでは、生成された CalibrationHelper のストライクはおおむね4%になっています。債券発行体は、金利がこれを下回ると、Call Optionを行使する事になります。
- Call Option の価格は、11.54% となっています(あくまで債券に内包している Call Option の価値であって、Call Option付債券の価格ではありません)。前の、バーミューダン・スワップションは、Payer Swaptionだったので、4%のストライクはdeep out of the moneyになっていました。しかし、ここでの債券のCall Optionは、債券発行体が持つオプションで、債券発行体にとっては、4%のストライクはdeep in the moneyになります。なので、オプション価格は元本対比、大きな値になります。
- oas100 すなわち、クレジットスプレッド=100bp のケースでは、生成された CalibrationHelper のストライクは、おおむね 3%になっています。これは、債券発行体にとって、スワップ金利が3%以下になった時に、すなわち自らの再調達コストが4%以下になった時にCall Optionを行使する事になるので、自動生成されたCalibrationHelperのストライクがそのように調整されたました。
- この場合のCall Optionの価格は、4.498%で、oas0のケースより小さくなります。In the Moneyの度合いが、少し小さくなった為です。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス