1. QuantLibを使ってみる
1.2 Example を試す
1.2.7 Gaussian1dModels : Gaussian Short Rate Model と Markov Functional Model
1.2.7.4 ソースコードの解析 (その1)
1.2.7.4.1 事前準備 : ローカル関数の定義(53~116行目)
main() 関数の前に、ローカル関数(このプロジェクト内でしか使えない関数)を2種類定義しています。このプログラム例の主目的は、GSRモデルと MFM の Calibration の方法を示す事です。なので、このローカル関数には、次の2つのような機能・役割を持たせています。
- calibrationBasket()関数により生成された CalibrationHelper 配列の画面出力(printBasket()) と
- calibrationの結果得られた、モデルパラメータの画面出力(printModelCalibration())
実際、このプロジェクトの実行結果となる画面出力には(前のセクション参照)、この2つの関数を使った出力表示が、何回も出てきます。
131行目以降は、メイン関数になり、以下にその内容を解説します。メイン関数内では、モデルのcalibration方法について、いくつかのテストを行っています。それぞれ、複雑な内容で、一挙に説明すると判りにくくなるので、先ほどの全体像で示したように、本体部分をいくつかのパートに分割して解説していきます。以下にコードに沿ってその手順を解説。
1.2.7.4.2 商品オブジェクトと、価格エンジンの作成 (131~225行目)
131~225 行目で、商品オブジェクト(NonStandardSwaptionクラスのオブジェクト)と、GSRモデルを使った価格エンジン(BasketGeneratingEngineクラスのオブジェクト)を作成しています。この2つのクラスの動作をテストする事が、このプロジェクトのメインの目的になります(クラスの詳細については、Appendix-1参照)。ちなみに、これらのオブジェクトは、これまでの例で説明した通り、それぞれ部品から作成し、それをコンストラクターに渡して組み立てます。
(1) 時価評価基準日の設定(131~132行目): 2014年4月30日に設定
(2) イールドカーブを2種類作成 (137~147行目):
Handle<YieldTermStructure> yts6m
Handle<YieldTermStructure> ytsOis ここでは、オプションモデルが想定する将来の金利の期待値となる、forecasting curve(yts6m)と、Payoffの期待値を現在価値に割り引く為の discounting curve(ytsOis)を、それぞれ別個に用意しています(いわゆる multi-curve対応)。但し、いずれのカーブもテスト用なので、シンプルに、2.5%と2%のフラットなカーブに設定されています。
(3) Volatility 曲面の作成(158~162行目):
以下の変数宣言で、スワップションのVolatility曲面を生成しています。
Handle< SwaptionVolatilityStructure> swaptionVolスワップション Volatility は、本来なら、"オプション行使期限"と、"対象スワップ期間"と、"ストライク金利"の3次元構造(一般的に Volatility Cube と呼ばれています)のデータになります。しかし、ここで使われているクラスは、対象スワップの満期日は共通(いわゆるco-terminal swaption)で、オプション行使期限と ストライク金利の2次元の曲面(Volatility Surfaceと呼ばれています)を格納するクラスになります。
(注 : 3次元の Swaption Volatilityを格納できる SwaptionVolatilityCube クラスは、QuantLibの中に存在するものの、未完成のようです。)
但し、ここで生成されたVolatility Surfaceは、単なるテスト用のフラットな平面で、一定値(20%)のBlack Volatilityに設定されています。
(4) 商品オブジェクトの作成(168~194行目) :
下記のコードが示す通り、商品(NonstandardSwaption)オブジェクトのコンストラクターに、部品として、対象スワップのオブジェクトと、オプション行使日のオブジェクトを渡し、商品オブジェクトを作成しています。具体的には、期間が10年のEuribor金利スワップを対象資産とするバーミューダンタイプのスワップションを生成しています。
auto swaption = ext::make_shared<NonstandardSwaption>(
underlying, :対象スワップのオブジェクト(184行目で作成済)
exercise :オプション行使日の配列(193行目で作成済)
); (5) GSRモデルの作成(200~216行目) :
Gsr クラスのコンストラクターに、部品を渡してモデルオブジェクトを作成しています。コードをみれば判る通り、コンストラクターへ渡す引数(部品)は、その前段階で、既に作成されています。
auto gsr = ext::make_shared<Gsr>(
yts6m, :中心回帰レベルθ(t)をフィットさせるforecasting curve。
stepDates, :piecewise constant(階段)関数 σ(t) のステップ日付
sigmas, :σ(t)の各ステップ期間の値(配列)
reversion :中心回帰強度α(t)を、ここでは定数値0.01で設定
); (6) PricingEngineを2種類作成(218~223行目) :
GSRモデルを使った価格エンジンオブジェクトを2種類作成しています。
― 218行目 : Gaussian1dSwaptionEngineクラスのオブジェクト。
このエンジンはシンプルなヨーロピアン・スワップションの価格計算用。
― 221行目 : Gaussian1dNonstandardSwaptionEngineクラスのオブジェクト。
バーミューダン・スワップションやCMSの価格計算用。
後者のエンジンは、“はじめに”でも触れた、BasketGeneratingEngine の派生クラスで、Calibration 用の特別な関数が定義されています。詳しくは、Appendix-1 で説明します。
ちなみに、それぞれの価格エンジンのコンストラクターと、そこに渡されている引数(部品)をソースコードから抜き出し、下記の通り若干の解説を加えました。引数の一部は、エンジンの部品というより、エンジンが行う価格計算アルゴリズムの中で使われるパラメータになっています。
auto swaptionEngine =ext::make_shared < Gaussian1dSwaptionEngine >(
gsr, :モデルとして、GSRモデルを使用
64, :数値積分を行う際の、離散化した積分区間の数
7.0, :数値積分を行う際の上下限(標準偏差の倍数)
true, :PayoffのExtrapolation(true=行う)
false, :PayoffのExtrapolationをFlatで行う(False=Flatにしない)
ytsOis :discounting curveの設定(OISを使用)
); auto nonstandardSwaptionEngine =
ext::make_shared <Gaussian1dNonstandardSwaptionEngine> (
gsr, :モデルとして、GSRモデルを使用
64, :数値積分を行う際の、離散化した積分区間の数
7.0, :数値積分を行う際の上下限(標準偏差の倍数)
true, :Payoffのextrapolation(true=行う)
false, :Payoffのextrapolationをflatで行う(行わない)
Handle<Quote>(), :債券の発行体のクレジットスプレッド
ytsOis :discounting curveの設定(OISを使用)
); (7) 最後に、商品オブジェクト(バーミューダン・スワップション)に価格エンジンを設定(225行目)
以上で、商品オブジェクトと価格エンジンの作成が終わりました。ただ、価格計算の前にGSRモデルのパラメータの calibrationが必要で、それが次のステップになります。
1.2.7.4.3 Naiveモードでの Calibration と価格計算(227~276行目)
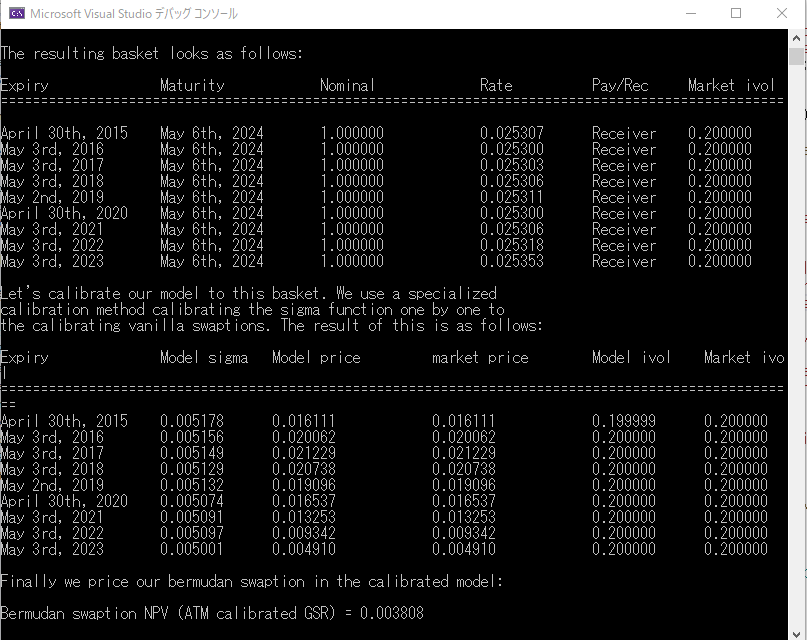
価格計算の前に、GSRモデルのパラメータを、ベンチマーク商品の価格(Volatility)を使ってCalibrationする必要があります。
これまでのプログラム例(”CallableBonds” と”BermudanSwaption”)では、Calibration のアルゴリズムで中心的な役割を果たす“CalibrationHelperオブジェクト”を、別途事前に作成し、それを最小値問題におけるコスト関数として使っていました(CalibrationHelperの役割については、CalibrationHelper クラスを参照)。 ところが、ここでは、NonStandardSwaption クラスのオブジェクトに備わっている calibrationBasket() 関数を呼び出し、そこで CalibrationHelper の配列を自動作成しています。また、この関数は、2通りの方法で、CalibrationHelper を生成する方法が備わっています。その2通りの内、一つ目の方法について、見て行きます。この方法は、Naïveと名付けられており、At the MoneyのスワップションのCalibrationHelperを自動生成します。
(1) まず、10年物の金利スワップの Index オブジェクトを作成(236行目)
(2) 次に calibrationBasket() 関数を使ったCalibrationHelperの自動生成
バーミューダン・スワップションの商品オブジェクト(変数名 swaption)から、calibrationBasket() 関数(この関数については、Appendix-2で解説)を呼び出し、CaibrationHelperを自動生成する(240行目)。この時、自動生成する2つの方法の内、Naïve法を指定している。
(3) (2)で生成された CalibrationHelper配列(変数名 basket)の各メンバーに価格エンジンを設定(254行目)
for (auto& i : basket)
i->setPricingEngine(swaptionEngine); 尚、ここで設定されている価格エンジンは、当初生成された2つの価格エンジンの内、シンプルなヨーロピアン・スワップション用の価格エンジンになります。(218行目参照)
(4) Calibrationの実行(257~262行目)
以下の通り、GSRモデルオブジェクトから、calibrateVolatilitiesIterative( ) 関数を呼び出し、calibrationアルゴリズムを走らせています。
Gsr -> calibrateVolatilitiesIterative(
basket, :CalibrationHelperの配列
method, :Solverオブジェクト(Levenberg-Marquardt 法)
ec :Solverの終了条件(end criteria)
); この関数は、piecewise constantなVolatility関数 σ(t) を、オプション期日の手前から順番にcalibration するアルゴリズムを実装しています。なお、257行目にある通り、Solverとして、QuantLibが用意している Levenberg Marquardt 法のアルゴリズムを使っています。
(5) 最後に、商品オブジェクトからNPV()関数を呼び出して、価格計算(272行目)
価格は、console 画面出力をみると、38.08bpとなっています。
以上のプロセスによる計算結果の画面表示を以下に再掲します。出力された数字の解説は、後程行います。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス