1. QuantLibを使ってみる
1.2 Example を試す
1.2.9 FittedBondCurve プロジェクト: 近似曲線を使った債券イールドカーブの構築
1.2.9.1 はじめに
イールドカーブの構築方法については、MulticurveBootstrapping や、他の Exampleプロジェクトの中で、何度か解説してきました。そこでのイールドカーブ構築方法は、Bootstrapping-Interpolation法と呼ばれる方法で、市場で観測される Par-Curve(Libor-Swap Curve)から、それに内包されている Discount Curve や Zero-Rate Curve、さらに Implied Forward Curve を導出する方法でした。このように導出されたイールドカーブは、デリバティブズの価格評価に必須の市場データであり、最も重要なイールドカーブ導出方法です。
一方で、このプロジェクトで紹介するイールドカーブの構築方法は、債券の利回りのように、期間とイールドを散布図で表示すると、下記グラフの様に綺麗に並んでいない場合に使われる方法です。債券の場合は、クーポンレートの違いや、流動性の違いから、期間が極めて近い債券同士でも、イールドがかなり異なるケースがみられます。こういった場合は、すべての点は通らないものの、パラメトリックな関数を使って近似曲線を描いて、債券市場全体のイールドカーブ形状を把握するする方が適切です。あくまで近似なので、そのイールドカーブを使って債券価格の Mark to Market をする事は出来ません。債券の場合、そもそも初めに市場価格ありきなので、イールドカーブを使って Mark to Market をする事自体ありません。
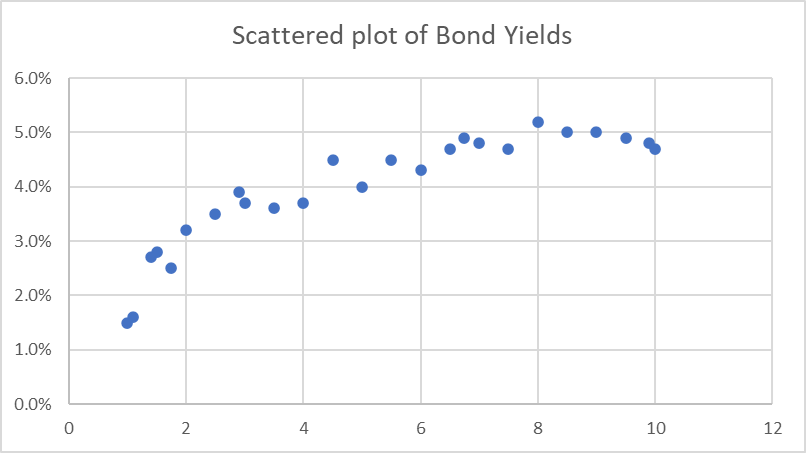
その様なイールドカーブは、この散布図から直接、パラメトリックな多項式を使って描く事も可能です。しかし、このプロジェクトで使われている7種類のイールドカーブの構築方法は、まず Discount Curve の近似曲線を求め、そこから間接的に債券利回り(par rate:債券価格がpar=100%になるようなクーポンレート)のイールドカーブを求めます。そのアルゴリズムを簡単にまとめて言うと、
- まずDiscount Curveを描く為の、パラメトリックな多項式を用意し、
- 次にイールドカーブを描く対象となる債券を複数特定し、その市場価格と利回りの情報を集め、
- 各債券のキャッシュフローをゼロクーポン債の集合と看做し、その価格を、1.のパラメトリックな多項式によるDiscount Curveを使って計算し、
- その価格を債券ごとに合計し、それ(近似されるDiscount Curveで評価した債券価格に相当)と、元の債券価格(市場価格)を比較して、その誤差(価格差の2乗)を計算し
- その計算をすべての債券で行い、誤差の合計を算出し
- その誤差の合計を最小にするような、近似曲線のパラメータを求めます。
- そうやって導出された Discount Curve から、債券の Par-Curve(価格=100となるようなクーポンレートを繋いだイールドカーブ)を求めます。
そうやって出来上がった近似曲線は、こういった感じです。
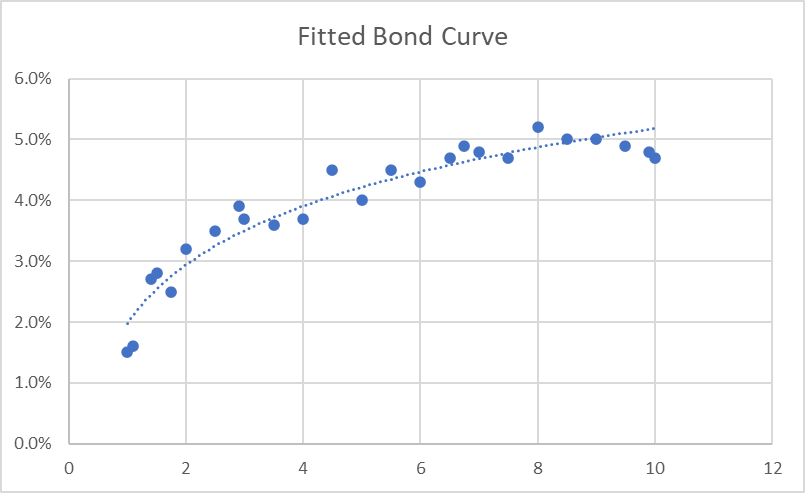
QuantLibでは、Discount Curve の近似曲線を描くパラメトリックな多項式を7種類用意し、FittedBondDiscountCurve::FittingMethod クラス(の派生クラス)の中でそれらを具体的に定義しています。このプロジェクトは、その FittingMethod のアルゴリズムをテストするプログラム例になっています。
ちなみに、その7種類のアルゴリズムは以下のようにネーミングされています。
(1) Exponential Splines
(2) Nelson-Siegel
(3) Svensson
(4) Cubic B-splines
(5) Simple polynomial
(6) Spread fitting
(7) Exponential splines with fixed kappa
この近似曲線によるイールドカーブ構築方法は、Bootstrapping-Interpolation 法のように、アービトラージフリーの制約下で厳密に構築されたものではなく、結局の所、債券イールドカーブの雰囲気を知る程度の役割しか果たしません。なので、使い道は限られます。また、カーブの表現力が少し違う点や、計算速度の違いはありますが、使う上で格段の優劣がある訳ではありません。これらのモデルの内、Nelson-Siegel や Svenssonモデルは、一部の中央銀行が、金融政策を遂行する上で、その国の国債市場のイールドカーブの特徴を把握する為に使っている様です。また、いくつかの証券会社のトレーディングデスクでは、これに類似した近似曲線を使って、債券の割安・割高を判断し、アービトラージ取引(厳密なアービトラージではなく、Convergence Trades と呼ばれている取引形態)に使っているようです。
尚、上記の7種類のアルゴリズムの内、Nelson-SiegelとSvenssonについては、「基礎編2.5 イールドカーブの構築方法(1)パラメトリック法」のセクションで簡単に解説しているので、参考にして下さい。
1.2.9.2 プロジェクトのビルド
これまでのプロジェクトと同様、まず”FittedBondCurve”プロジェクトのソースコードをビルドします。
- QuantLib のディレクトリ下にあるソリューションファイル "QuantLib.sln" を開けます。すると、Visual Studio が起動され、このソリューションファイル下にあるプロジェクトがオープンされます。ソリューションエクスプローラー画面にある 21 個のプロジェクトファイルの中から、FittedBondCurve プロジェクトを選択します。
- FittedBondCurve プロジェクトのディレクトリを展開し、SourceFiles のフォルダーにある "FittedBondCurve.cpp" をクリックすると、約 680行あるソースコードが開かれます。
- メニューバーから “プロジェクト(P)” → “スタートアッププロジェクトに設定(A)” を選択します。これで、QuantLib.sln の中で、最初に FittedBondCurve プロジェクトのメイン関数が呼び出されます。
- 同じくメニューバーから、 “プロジェクト(P)” → “プロパティ(P)” を選択し、これまでのプロジェクトと同様、boost ライブラリへのパスを設定します。(実践編1.1.5 “QuantLibソリューションのビルド”の解説を参照)
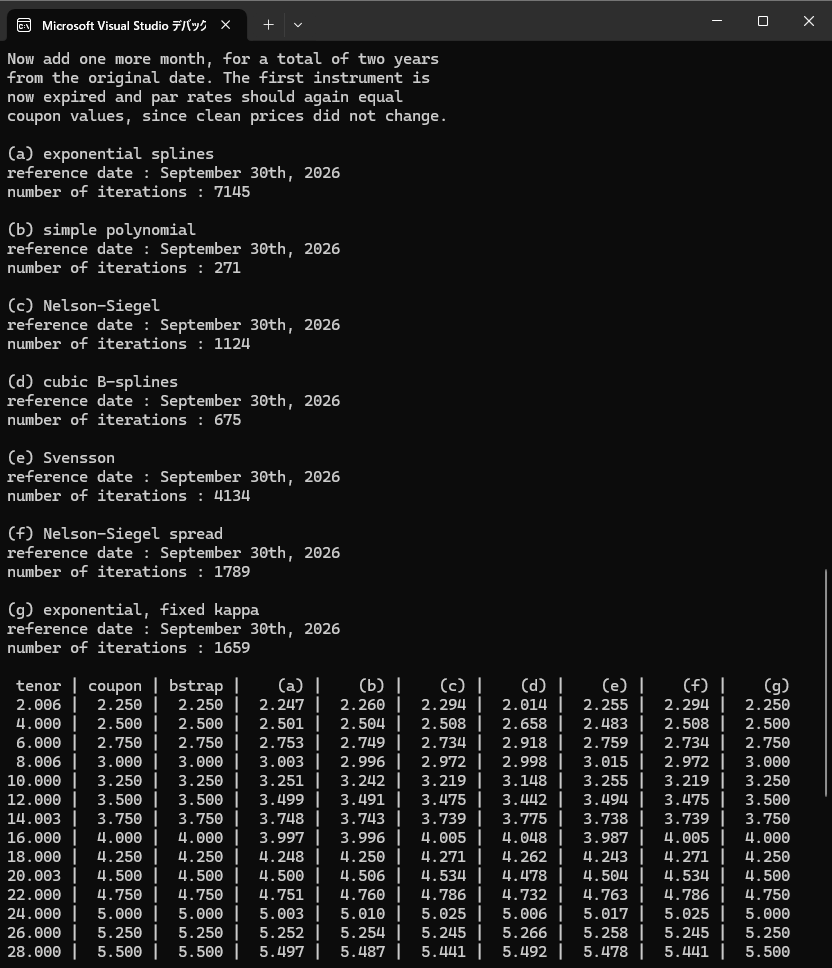
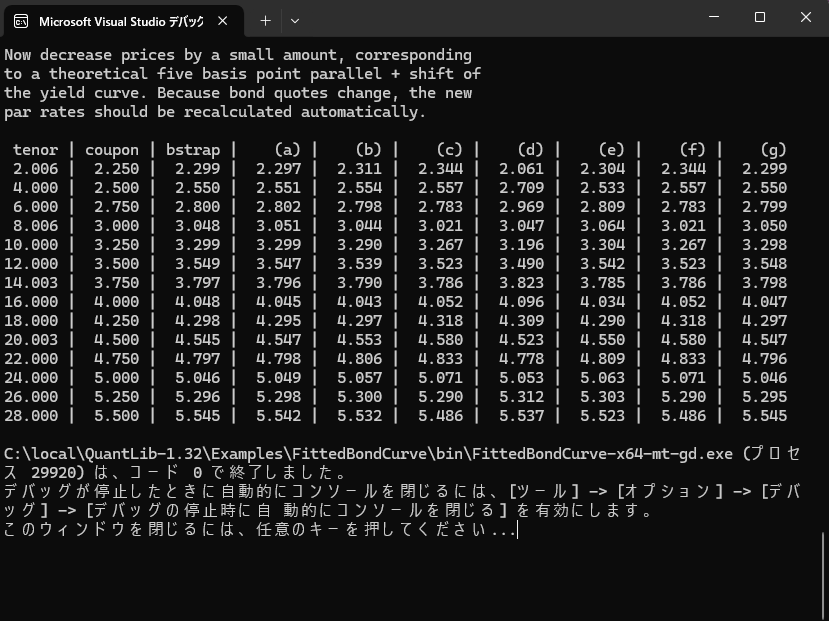
- メニューバーから "ビルド" → "FittedBondCurve のビルド" を選択するとビルドが開始されます。エラー無くビルドが正常終了すれば、試しにプログラムを走らせてみます。メニューバーの "デバック" → "デバックの開始" を選択し、下記のConsole画面が出力されれば成功です。
(注:プログラムが終了すると同時にConsole画面も消えてしまうようであれば、"ツール" → "オプション" → "デバック" → "全般" とし、「デバックの停止時に自動的にコンソールを閉じる」 のチェックボックスをオフにする。)
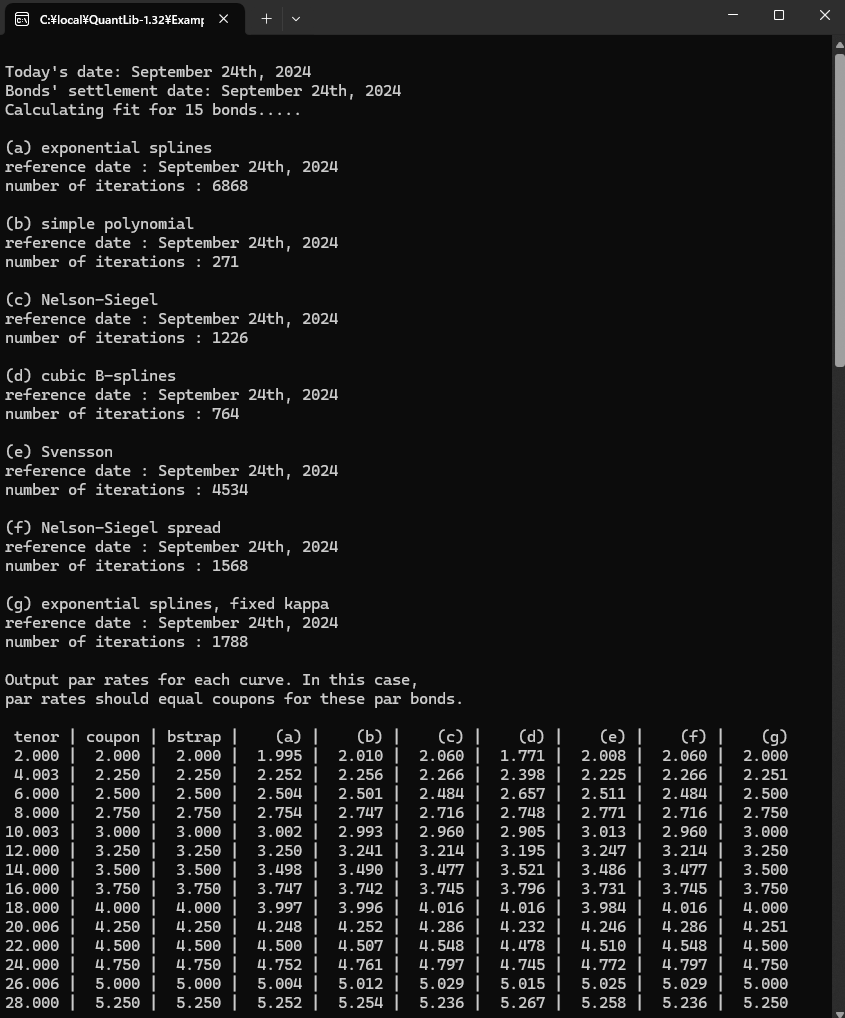
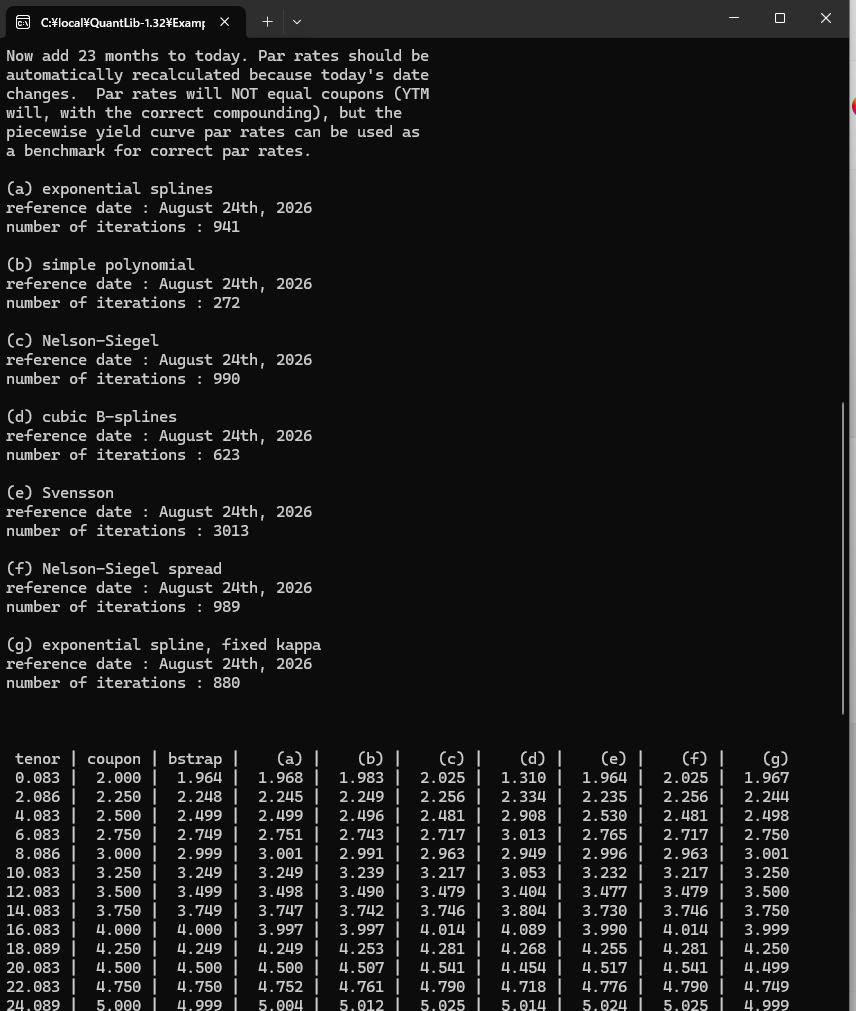
1.2.9.3 ソースコードの全体像
このプロジェクトのソースコードは、"FittedBondCurve.cpp" になります。この解説はそのソースコードを見ながら読み進めてください。それをブラウザーでも見れるように、htmlファイルに変換したソースコードを載せておきます。
さて、ソースコードは見ての通り、約 680行あります。その構成は、
| ― | プリプロセッサー | (1~48行目) |
| ― | ローカル関数の定義 | (51~76行目) |
| ― | メイン関数 | (79~678行目) |
| ・ 本体 | (81~668行目 try{}で囲まれた部分) | |
| ・ 例外処理 | (670~676 catch{}部分) |
と成っています。
ローカル関数は、parRate() と printOutput() の2種類が定義されています。前者は、discount curve から、債券の Par Rate(債券価格が額面に対しpar=100% になるようなクーポンレート)を導出する関数です。式で表すと、下記のようになり、discount curve から、スワップ金利の Par Rate を導出するのと、同じ式を使っています。
\[ C=\frac{D(T_0)-D(T_M)}{∑_{i=1}^M ΔT_i~D(T_i)}, ~~~~~但し~~D(T_i)~は~T_i~ 時に対応する~discount factor, ~~ ΔT_i=T_i-T_{i-1} \]また、後者は、
- テストされる FittingMethod の種類と、
- Reference Date(カーブのスタート時を決める参照日付)と
- Solver による iteration の数(最適化問題を解く為に計算された、for loop内での再帰計算回数)
を、Console 画面出力する関数です。
次に、メイン関数の本体部分は、以下のような構成になっています。
- まず債券の市場データの準備。2~30年満期の債券を15種類用意し、それぞれクーポンレートと市場価格を設定。その情報を元に、BondHelper オブジェクトを作成。
- 1.の情報を元に、2 種類のイールドカーブオブジェクトを作成。一つ目は、Bootstrapping-Interpolation 法を使ったイールドカーブ。2つ目は、今回テストされる FittingMethod を使ったイールドカーブで、これは 次にある通り、FittingMethod を特定してから具体化されるもの。
- 2.で作成したイールドカーブの内、後者に対して、7種類のFittingMethodを設定し、7種類のイールドカーブオブジェクトを作成。
- FittingMethod によって作成された Discount Curve から、債券の Par Rate を導出し、それを画面出力(前出のコンソール画面出力参照)
- 3.と 4.と同じ操作を、Reference Date などの情報を若干変えて、何通りか行う。
この全体像を踏まえながら、次にソースコードの中味を解説していきます。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス