基礎編 ６． クレジットデリバティブズ
6.3 クレジットデフォールトスワップの価格計算方法
6.3.1 CDSの価格計算式の導出
このチャプターの“はじめに”のセクションで、一般的な金融商品の価格式を示しました。その式が示すのは、すべての金融商品の価値は、将来のキャッシュフローの金額に発生確率を掛けそれを現在価値に割り引いたものになるという事です。言い換えると、将来発生するキャッシュフローの期待値合計になります。その時示した式を再記します。
\[ Present~~Value~~of~~Financial~~Instruments~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ =\sum CashFlow_i(T_i)×Probability(CashFlow_i)×DiscountFactor(T_i) \]CDSの場合、Protection LegのCash Flowと、Premium LegのCash Flowの交換になるので、両者のプラスマイナスの符号を逆にして右辺に置けばCDSの価値になります。契約の開始時では等価交換になるので、その価値は0になります。但し、現在主流の標準的な契約形態では、Premium Legのクーポンレートが事前に固定されているので、必ずしもそうならず、その場合は、契約時に現金授受を行って、等価交換になるように調整します。
この式を、論文などで使われている、もう少し厳密な表記方法に変えてみましょう。その為にProtection LegとPremium Legを分けて考えます。まずPremium Leg Cash Flowから。
(1) Premium Leg Cash Flowの期待値
Premium Leg のキャッシュフローは、Protection BuyerがProtection Sellerに対して、みなし元本に一定のpremiumレートを掛けた金額を、定期的に、満期日まで支払うものです。但し、もしcredit eventが発生した場合は、その時点でのpremiumの経過利息相当額を支払って、それ以降の支払い義務が終了します。
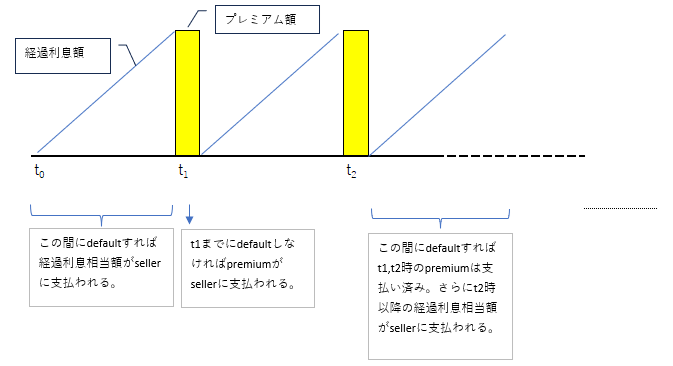
なので、Premium Legの期待値は、Credit event発生時に、それ以前までに支払ったプレミアムの期待値に、その時点での経過利息支払い額の期待値を加えたものです。計算は、プレミアムキャッシュフロー期待値と、credit event発生時の経過利息相当額の期待値をそれぞれ別個に行います。
(1)-1 Premium CF の期待値
まず、定期的に支払われるキャッシュフローの期待値は、下記式で求まります。なお、以下に示す価格式はすべて“みなし元本額”を１と置いています。
\[ \begin{align} Value~~ & of~~ Premium~~ CF=\sum_{i=1}^n c×Δt_i×\mathbb{Q}(t_i)×D(t_i)~~~~~~~~~~~~~~~~~\\ 但し & \\ & c~ ：~プレミアムレート（年率％） \\ & t_i,~i=1,…,n~ ：~プレミアム支払日。但し~ t_n=T は~ CDS~の満期日。t_0＝現在\\ & Δt_i=t_i-t_{i-1}~ ：~プレミアム支払い期間（年）。\\ & \mathbb{Q}(t_i)~ ：~ t_i~ 時までのサバイバル確率~ （ t_i ~ 時までcredit~eventが発生しない確率）\\ & D(t_i)~ ：~ t_i ~ 満期のゼロクーポン債価格（=Discount~ Factor） \end{align} \]ディスカウントファクター\(D(t)\)は、リスクフリー金利のイールドカーブから導出します。また、ｔ 時までのサバイバル確率\(\mathbb{Q}(t)\) は、クレジットカーブから求めますが、それが具体的にどのような関数形になるかは、後で解説します。とりあえず今は、\(\mathbb{Q}(t)\) のままで、話を進めます。
(1)-2 credit event発生時の経過利息支払い額の期待値
次に、credit event発生時までの経過利息相当分の期待値を求めます。
その為にまず、各プレミアム期間を微小時間（δt）で区分し、各区分内で credit event が発生する確率を求めます。ある微小時間（δt）内で credit event が発生する確率ですが、この確率は、t 時までに default せず、そこから t+δt までの間に初めて default する確率になります。先ほどの式で使った\(\mathbb{Q}(t)\)は、t時まで default しない確率なので、\(1-\mathbb{Q}(t)\) が t 時までに default する確率（累積分布確率）になります。なので、それを t で微分すれば、t という瞬間に default する確率（確率密度）になります。それをとりあえず、下記式で表記します。
\[ t時にデフォールトする確率密度=\frac{d(1-Q(t)}{dt}=- \frac{dQ(t)}{dt} \]（注：\(\mathbb{Q}(t)\) は時間軸に対し、単調減少関数なので、時間で微分すると必ずマイナスになります。上記右辺はそれにマイナス符号が付いているので、必ずプラスになり、確率密度の必要条件を満たします。）
次に、credit event が発生した時点の経過利息相当額を求めます。Credit event の発生時を \(\tau\) と置くと、\(\tau\) が\((t_{i-1},t_i)\) 区間内にある場合の経過利息相当額は \(c×(\tau -t_{i-1})\) となります。この値に先ほど求めた確率密度を掛け、さらに \(\tau\) 時の割引率\(D(\tau)\)を掛けて、それをクーポン期間内で積分すれば、あるクーポン期間\((t_{i-1},t_i)\)内での期待値が求まります。式で表すと下記のようになります。
\[ \int_{t_{i-1}}^{t_i} c×(τ-t_{i-1})×D(τ)×\left(- \frac{d \mathbb{Q}(τ)}{dτ}\right)dτ \]さらにこれを、全クーポン期間で足し上げれば、credit event発生時に支払うべき経過利息相当額の期待値になります。式で表すと、下記の通りです。
\[ Value~~ of~~ AccruedPayment=\sum_{i=1}^n c\int_{t_{i-1} }^{t_i} (τ-t_{i-1})D(τ)\left(-\frac {d\mathbb{Q}(τ)}{dτ}\right)dτ \](1)-3 Premium CFの期待値
そして上記の(1)-１ の式と(1)-２ の式を足せば、Premium Leg cash flowの期待値になります。
\[ \begin{align} Premium~~ Leg & =~Premium~CF~+~ AccruedPayment \\ & =\sum_{i=1}^n c\left[Δt_i \mathbb{Q}(t_i)D(t_i)+\int_{t_{i-1}}^{t_i} (τ-t_{i-1}))D(τ)\left(-\frac{d\mathbb{Q}(τ)}{dτ}\right)dτ \right] \end{align} \]
(2) Protection Leg の期待値
Protection Leg cash flow は、credit event が発生した場合にのみ発生します。その期待値は、下記のように計算すれば求まります。
- CDS の満期日までを微小時間で区切って、各時間での credit event 発生確率を求め、
- それに Loss given default 額 （Protection Buyer が seller から受け取れる金額）の期待値を掛け
- それに各時点のDiscount Factorを掛けて現在価値に換算し、
- さらにそれを現在から満期まで積分
微小時間 dτ 内での credit event 発生確率は、先ほど求めた\(-d\mathbb{Q}(τ)/dτ\) になります。なので、
\[ Protection~~ Leg=\int_0^T E[LossGivenDfault(τ)]×D(τ)×\left(-\frac{d\mathbb{Q}(τ)}{dτ}\right)dτ \]となります。
(3) CDS の価格
CDSの価値は、(1) (2)で導出した Premium Leg と Protection Leg の期待値の合計になります。但し、スワップなので、いずれかがプラスで、その逆がマイナスの符号になります。仮に、Protection Buyer（Protection Legの受取、Premium Legの支払い）の立場で、価格式を考えると、
\[ \begin{align} CDS Value & = +~Protection~~ Leg~-~Premium~~ Leg \\ & =+~ 0.6\int_0^T D(τ)\left(-\frac{d\mathbb{Q}(τ)}{dτ}\right)dτ \\ & ~~~~~ -~\sum_{i=1}^n c\left[Δt_i \mathbb{Q}(t_i)D(t_i)+\int_{t_{i-1}}^{t_i} (τ-t_{i-1})D(τ)\left(-\frac{d\mathbb{Q}(τ)}{dτ}\right)dτ\right] ,\\ & 但し~~ T=t_n \end{align} \]となります。（Protection Seller にとっての価値は、± を逆にすればよい）
これで一応、CDS の価格式が導出できました。しかし、ここから実際に価値を計算するには
(1) サバイバル確率 \(\mathbb{Q}(t)\) をどのように求めるのか
(2) 式の中にある積分の計算を、どのように求めるのか
を決めなければなりません。なので、次にその説明に進みます。