実務で使える金融工学　上級編

上級編　６．　 Libor Market Model　

6.3  古典的なLMMの拡散項係数（Volatility関数）

6.3.4   Volatility の期間構造の時間経過による推移

6.3.4.1   Volatilityの期間構造の推移がどうあって欲しいか？

前のセクションで説明した Cap/Floor 価格に含まれる Black Volatility の期間構造は、現時点からオプション行使日まで一定という前提で導出されたものです。しかし、Volatility の期間構造の形状が観測される理由からすれば、フォワード Libor の Volatility が、最初から最後まで一定と仮定するのは無理があります。時間の経過に伴いフォワード Libor の残存期間が短くなるにつれ、中心回帰の影響が減少していく一方、中央銀行の金融政策の影響をより強く受けるようになります。すると、Volatility の水準は一定ではなく、フォワード Libor の残存期間によって変化すると予想するのが自然です。その様子をコントロールするのが、Volatility 関数の中の、\(ψ(t,T_i)\) になります。　\(ψ(t,T_i)~は、観測時~~t~~と~~Libor~~の期日~T_i\) に依存し（言い換えると、Libor の残存期間 \(T_i-t\) に依存し）時間の経過に伴う Volatility の期間構造（カーブ）の推移を表現します。 

描こうとするイメージは下記のグラフのようなものです。時間の経過により、残存する Libor の数が減ってくるので、カーブはだんだん短くなっていきますが、カーブの手前は高く、そこから少し上昇した後、緩やかに低下していくような形状を維持したままです。最長期の Libor の Volatility だけを見れば、最初は低く、だんだん高くなっていき、最後に少し低下するようなイメージです。また、当初ピークをつけていたゾーンのVolatilityは、残存期間がゼロに近づくにつれ、低下していく事が想定されます。下のグラフの赤点線がまさに \(ψ(t,T_i)\) で描きたい曲線です。　　 

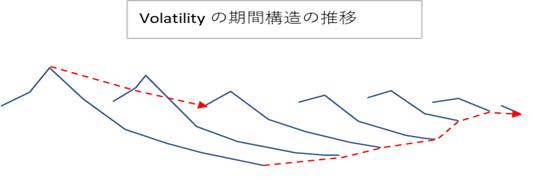
この期間構造の推移は、Libor 金利が変動する要因から、こう動くのが経済合理的であろうという推察で描きましたが、そのような主観的な想定だけをベースに Volatility 関数を決める訳にはいきません。期間構造の推移も、ベンチマーク商品の市場価格に内包されている、将来のVolatilityの予想を、ある程度織り込む必要があります。 

Volatility の期間構造が、将来どのように動くかは、Cap の市場データから直接読み取る事はできません。この時間の推移による形状変化の情報は、金利オプション市場のもうひとつの重要な商品である、Swaption 価格に内包されており、そこから読み取る事になります。Swaption の対象資産は、長期の金利スワップ取引であり、Libor を直接の対象資産とはしていませんが、スワップ金利と Libor 金利との密接な関係から、LMM による Libor 金利の確率過程から、スワップ金利の確率過程も近似的に記述する事ができます。そこから、Libor の Volatility カーブの時間による推移の情報も取り出す事ができます。ただ、内包されている将来の Volatility カーブの予想が、上のグラフのように、きれいな形になっている保証は全くありませんが。 

いずれにしても、スワップション価格から Volatility カーブの推移の情報を読み取る方法を説明する前に、まず LMM の確率過程から、どのようにして スワップ金利の確率過程を近似するのか、みてみます。 

6.3.4.2   Rebonatoの公式

まず、Swaption の対象となるフォワードスワップ金利は、下記式のようにスワップキャッシュフロー期日を満期とするゼロクーポン債価格の集合で表現できます。 （有名な公式で、その導出過程は、基礎編 ”Annuity と Discount Factor とスワップ金利の関係”で解説しているので、そちらをご覧ください。）

\[ SwapRate(t,T_s,T_e)=\frac{P(t,T_s)-P(t,T_e )}{\sum_{i=s+1}^e τ_i~ P(t,T_i)} =\frac{1-FP(t,T_s,T_e)}{\sum_{i=s+1}^e τ_i~ FP(t,T_s,T_i)} \tag{6.41} \]

但し、 

• \(t\) : 現時点
• \(SwapRate(t,T_s,T_e)~~~：~~~t~~時における~~T_s~~スタート、T_e~~エンド日のフォワードスワップ金利\)
• \(T_i~~~:~~~スワップのキャッシュフロー日~~i=s+1~,~s+2~,~…~,~e\)　で \(e-s-1\) はスワップで発生するキャッシュフローの数（変動と固定で同じと仮定）
• \(P(t,T)~~~:~~~t~~時における~~T~満期ゼロクーポン債の価格\)
• \(FP(t,T_s,T_i)~~~:~~~T_i~満期のゼロクーポン債の、t~時における~~T_s~フォワード価格\)
• \(τ_i~~~:~~~スワップのキャッシュフロー間の期間、すなわち~~T_i-T_{i-1} \)

そして、式中にあるフォワードゼロクーポン債価格は、下記のようにフォワード Libor のベクトルを使っても表現できるのでした。 

\[ FP(t,T_s,T_i)=\frac{P(t,T_i)}{P(t,T_s)}= ∏_{j=s+1}^i FP(t,T_{j-1},T_j) = ∏_{j=s+1}^i \frac {1}{1+τ_j L_j (t)} \]

すると、フォワードスワップ金利自体が、フォワード Libor のベクトルを使って表現できます。 

\[ SwapRate(t,T_s,T_e)=\frac{1-FP(t,T_s,T_e)}{∑_{i=s+1}^e τ_i~ FP(t,T_s,T_i)} =\frac{1-∏_{j=s+1}^e \frac{1}{1+τ_j L_j (t)}}{∑_{i=s+1}^e τ_i~ \left(∏_{j=s+1}^i \frac{1}{1+τ_j L_j (t)} \right) } \tag{6.42} \]

上の式を見れば判る通り、スワップ金利が、フォワード Libor 金利のベクトルの関数になっています。しかし、Libor が分子と分母の両方に現れており、スワップ金利が Libor の単純な線形結合で表現できる訳ではあありません。 

これを、別の表現方法に変換します。式を解析していくプロセスは省略し、結果のみ示します。 

\[ SwapRate(t,T_s,T_e)=\frac{1-FP(t,T_s,T_e)}{∑_{i=s+1}^e τ_i~ FP(t,T_s,T_i)} =∑_{i=s+1}^e ω_i(t)L_i(t) \\ ω_i (t)=\frac{τ_i~ FP(t,T_s,T_i)}{∑_{j=s+1}^e τ_j~ FP(t,T_s,T_j)}~~~~~~~~ \tag{6.43} \]

この式は、Rebonato により示されました（Rebonato “On the pricing implications of the joint lognormal assumption for the swaption and cap markets” 1999）。Rebonato は、この式から、フォワードスワップ金利はフォワード Libor の加重平均と見做せると考えました。\(ω_i (t)\) がそのウェイトになります。しかし、ウェイト \(ω_i (t)\) の式中にある \(FP(t,..)\) 自体が、フォワード Libor　\(L_i (t)\)　の関数になるので、\(L_i(t)\) が動けば、ウェイトも変動してしまいます。そこで、Rebonato は、\(ω_i (t)\) を現在（t＝0）の値で固定し、それを \(ω_i (t)\) の近似値と見做しました。\(ω_i (t)\) の分母と分子に \(FP(t,..)\) があり、両方が高い相関を持って確率変動するので、その比は初期値と大きく変わらないだろうという発想です。（実際には、微妙に変動しますが、Libor の変動に比べれば、微小な変動に留まります。Rebonato らは、実際にそれを検証しています。）　すると \(ω_i (t)\) の近似値は以下のように表現できます。 

\[ ω_i (t) ~ \simeq ~ ω_i (0)~ = \frac{τ_i~ FP(0,T_s,T_i )}{∑_{j=s+1}^e τ_j~ FP(0,T_s,T_j )} \tag{6.44} \]

これを6.43式に代入した上で、両辺を微分します。 すると、スワップ金利のSDEと、フォワードLibor金利のSDEの関係性が見えてきます。

\[ d~SwapRate(t,T_s,T_e )~ \simeq ~ ∑_{i=s+1}^e ω_i (0)~dL_i (t) \]

この左辺を、Black Model で表現し、一方、右辺の \(dL_i(t)\) を LMM で表現します（確率測度は任意のフォワード測度 Q とします）。すると下記のような近似式が導出できます。 

\[ \begin{align} drift(…)dt & +BlackVol_{swap} ~S(t)~dw^Q \\ & \simeq ~ ∑_{i=s+1}^e ω_i (0)~(drift(…)dt+ϕ_i~ψ(t,T_i)~L_i(t)~ {\bf c_i(t)∙dw^Q }) \tag{6.45} \end{align} \]

(注；左辺と右辺のドリフト項はそれぞれQ測度下でアービトラージフリーになるような値になりますが、ここでは拡散項係数にのみ注目するのであえて特定せず、単にdrift(…)と置いています) 

ここから、下記式のように、スワップ金利の（瞬間）2 次変分を、スワップ金利を構成する Libor 金利の（瞬間）共変分の線形結合として導出できます。 

\[ \begin{align} \langle d SwapRate∙ d SwapRate \rangle & =BlackVol_{swap}^2 S(t)^2 dt \\ & \simeq \left(\sum_{i=s+1}^e w_i(0)ϕ_iψ(t,T_i)L_i(t){\bf c_i (t)}\right) \left(\sum_{j=s+1}^e w_j(0)ϕ_jψ(t,T_j)L_j (t){\bf c_j (t)}\right) dt \\ & =\sum_{i,j=s+1}^e ρ_{i,j}\left(w_i(0)ϕ_iψ(t,T_i)L_i(t)\right) \left(w_j(0)ϕ_jψ(t,T_j)L_j (t) \right)dt \tag{6.46} \end{align} \]

そして、この式の両辺を、\(t＝0\) から \(T_s\) （オプション行使日＝対象スワップのスタート日）まで積分すれば、Black モデルでのスワップ金利の分散が、LMM でのフォワード Libor 間の共分散で表現できる事が判ります。すなわち 

\[ \begin{align} &∫_0^{T_s} BlackVol_{swap}^2 SwapRate(t)^2 dt \\ & \simeq∫_0^{T_s} \left[ \left( ∑_{i=s+1}^e w_i(0)ϕ_iψ(t,T_i)L_i(t) {\bf c_i(t)}\right) \left(∑_{j=s+1}^e w_j(0)ϕ_jψ(t,T_j)L_j(t){\bf c_j (t)} \right) \right] dt \tag{6.47} \end{align} \]

ここで、両辺の拡散項係数にある \(S(t)~と~L_i (t)\) もついでに \(t=0\) 時の値で固定します。これらも、高い相関を持って動くので、確率変動してもその比は大きく動かないであろうという発想です。　すると、左辺の積分が解けて、右辺の積分から定数部分を積分の外に出すと、下記式のように、Black Volatility と LMM の拡散項係数の関係式が導出できます。（左辺に出てくる \(T_s\)を右辺に移しています。） 

\[ \begin{align} (Black & Vol_{swap})^2 ~ \\ &\simeq ~ \frac{1}{T_s}∑_{i,j=s+1}^e \frac{ω_i(0)~ ω_j(0)~ L_i(0)~ L_j(0)}{SwapRate(0,T_s,T_e)^2 } \int_0^{T_s} ρ_{i,j}(t)(ϕ_i ψ(t,T_i))(ϕ_j ψ(t,T_j))dt \tag{6.48} \end{align} \]

この式は、“Rebonatoの公式”と呼ばれています（Brigo-Mercurio本2006年　p283）。左辺のスワップ金利の分散が、右辺のフォワード Libor 間の（最終）共分散（Terminal Covariance）の線形結合で近似できるという点に着目してください。右辺の積分が、フォワード Liborの変化率の、（最終）共分散に相当します。 

6.3.4.3   スワップション価格から、Libor Volatility の推移を導出する方法

さて、以上のように、スワップションの Implied Black Volatility と、LMMにおけるフォワード Libor の Volatility の関係が、近似できると判ったところで、スワップション価格から Libor の Volatility の期間構造の推移を読み取れるという事を示します。 

ここで、行使日が異なるが、対象スワップの満期が同じ２つのヨーロピアン・スワップション（co-terminal swaption）を考えます。１つめのスワップションの行使日を　\(T_{s1}\)、２つめの行使日を \(T_{s2}\) とし、対象スワップの満期日は、いずれも \(T_{s3}\) とします。各スワップションの対象スワップの金利を \(SwapRate(0.T_{s1},T_{s3}),~~SwapRate(0.T_{s2},T_{s3})\) とおき　Implied Black Volatilityを \(SwapVol_{s1}~~~ SwapVol_{s2}\)　とします。これを、6.48 式に代入すると。 

\[ \begin{align} & (SwapVol_{s1})^2 \\ & \simeq \frac {1}{T_{s1}} ∑_{i,j=s2}^{s3} \frac{ω_i (0)~ ω_j (0)~ L_i (0)~ L_j (0)}{SwapRate(0,T_{s1},T_{s3})^2} \int_0^{T_{s1}} ρ_{i,j}(t)~(ϕ_i~ ψ(T_i-t))(ϕ_j~ ψ(T_j-t))dt \tag{6.49} \end{align} \] \[ \begin{align} & (SwapVol_{s2})^2 \\ & \simeq \frac{1}{T_{s2}} ∑_{i,j=s3}^s3 \frac{ω_i(0)~ ω_j(0)~ L_i(0)~ L_j(0)}{SwapRate(0,T_{s2},T_{s3})^2 } \int_0^{T_{s2}} ρ_(i,j)(t)~(ϕ_i~ ψ(T_i-t))(ϕ_j~ ψ(T_j-t))dt \\ & \simeq 1/T_{s1} ∑_{i,j=s3}^{s3} \frac{ω_i(0)~ ω_j(0)~ L_i(0)~ L_j (0)}{SwapRate(0,T_{s2},T_{s3})^2} \int_0^{T_{s1}} ρ_{i,j}(t)~(ϕ_i~ ψ(T_i-t))(ϕ_j~ ψ(T_j-t))dt \\ & + \frac{1}{(T_{s2}-T_{s1})} ∑_{i,j=s3}^{s3} \frac{ω_i(0)~ω_j(0)~L_i(0)~L_j(0)}{SwapRate(0,T_{s2},T_{s3})^2} \int_{T_{s1}}^{T_{s2}} ρ_{i,j}(t)~(ϕ_i~ψ(T_i-t))(ϕ_j~ψ(T_j-t))dt \\ & ~ \tag{6.50} \end{align} \]

長い式で分かりにくいですが、ここで言いたいのは、２つのスワップション価格から、　\(L_{s3}~（T_{s2}~スタートで~T_{s3}~エンドのフォワード~ Libor~）~の~T_{s1}~から~T_{s2}\) の間の（すなわち将来の） Volatility の情報が取り出せるという事です。最後の式の第 2 項（フォワードLibor　\(L_{s3}~の（瞬間）分散を~T_{s1}~から~T_{s2}\) まで積分）が、まさにそれです。 

6.3.4.4   Volatility 関数　\(ψ(t,T_i )\)　の形

Volatility の期間構造、特にその時間経過による推移の様子に関する情報が、市場データのどこに含まれているかわかった所で、いよいよその関数形をどう特定するかについてみてみます。関数形を決めてしまえば、あとはそのパラメータを、先ほど説明した市場データに Calibration すれば、関数形が完成します。 

\(ψ(t,T_i)~~あるいは~~ ϕ_i~ψ(t,T_i)\) の関数形をどのように置くかについては、大きく分けて２つの方法があります。ひとつは、パラメトリックな指数関数を使って、期間構造の形状を表現する方法で、もうひとつは、\(ϕ_i~ψ(t,T_i)\) を、Libor ごとに、離散的な時間軸上で Piecewise Constant な関数とみなし、Liborのテナー軸と時間軸からなる Piecewise Constant　な行列で表現する方法です。 

パラメトリックな指数関数を使う方法は、Volatility　の期間構造を、前のセクションで示した望むような形状で描き、かつ時間が経過しても維持し続けます（斉時的）。またパラメータの数が少なくて済み、Over-Specification　の問題が小さくて済みます。一方で、CAP　と　Swaption　の両方の市場価格へ　Calibration　しようとすると、市場価格との誤差（Calibration Error）が、おおきくなりがちです。Piecewise Constant　な行列で表現する場合、市場データへのフィットは格段に良くなりますが、Over-Specification　の問題も大きくなります。また、期間構造の曲線が、市場データに合わせると、必然的に不自然なでこぼこが発生します。また、制約条件をうまくかけないと、経済的に意味のない数字（マイナスや虚数のVolatility）になる可能性があります。 

それぞれの関数形について、もう少し詳しくみてみます。　 

 

（i）  Rebonatoの4パラメータの指数関数形 

Rebonato は、\(ψ(t,T_i)\) として、そのカーブを描くパラメトリックな関数を仮定し、そのパラメータを、Cap の市場価格に Calibration して求める方法を提示しました。具体的には、\(a,b,c,d\) ４つのパラメータを使った、下記のような形の指数関数です。 

\[ \begin{align} ψ(t,T_i;a,b,c,d) & =(a(T_i-t)+d)~ e^{-b(T_i-t)}+c \\ & =(aτ+d)~ e^{-bτ}+c,~~~~~ \\ & τ=T_i-t \tag{6.51} \end{align} \]

この関数形は、パラメータ \(a,b,c,d\) の取り方によって、Volatility の期間構造が、前のセクションで示したような、短期から中期へ向かって一旦上昇しその後低下するような形状を描く事ができるし、単調減少するような形状も表現できます。また \(ψ\) が各 Libor の残存期間 \(τ=T_i-t\) のみに依存するので、Volatility カーブが、当初の形状を維持したまま推移する事になります（斉時的）。言い換えると当初のカーブが、時間の経過に伴い残存 Libor の数が減るにつれ、右端から順番に短くなっていくイメージです。パラメータ \(a,b,c,d\) は、Cap の市場価格に内包している当初 Volatility の期間構造に Calibration して求めます。さらに、フォワード Libor 毎のパラメータ \(ϕ_i\) を組み合わせて使えば、Calibrationする際に、Cap価格をきちんと再現できるようなVolatility関数を導出できます。しかし、CapとSwaptionの両方にCalibrationしようとすると、関数形の制約が強すぎて、誤差が大きくなる傾向があります。 

 

(ii)   Piecewise Constantな行列で表現 

もうひとつの方法は、Volatility 関数　\(ϕ_i~ ψ(t,T_i)\)　を、離散的な観測時間軸 \(t_j\) と、Libor のテナー軸 \(T_i\) からなる定数パラメータの行列としておき、そのパラメータを Swaption の市場価格（および Cap の市場価格）に Calibration して求める方法です。 

\[ ϕ_i~ψ(t_j,T_i )=[{\bf G}]=\left[ \begin{array}{ccc} g_{1,1} & 0 & 0 \\ \vdots & \ddots & 0 \\ g_{n,1} & \dots & g_{n,m}\\ \end{array} \right] ~~~~ i=1,2,...,n~~~j=1,2,...,m \tag{6.52} \]

行ベクトルは、フォワード Libor (\(L_i\))ごとに設定する、Piecewise Constant な Volatility 関数（要は定数のベクトル）に相当します。一方、列ベクトルは、離散化した各時点 \(t_j\) における Volatility の期間構造に相当します。（前のセクションの Volatility の期間構造の推移のグラフで、列ベクトルが、実線のカーブの推移を示し、行ベクトルが、点線を示します）　各パラメータは、Libor の期日が到来するまで有効なので、上の行列の下三角の要素のみ使用されます。フォワード Libor の数は最大 80~160 個あり、また時間軸も、モンテカルロシミュレーションで離散化する場合は、少なくとも Libor の期間で区切る必要があるので、最終的に ｎ × ｍ は、かなり高次元の行列になります。しかし、そのままではパラメータ数が多すぎで、Over-Specification の問題が大きく、Calibrationの計算時間も膨大になります。実際には ｎ と ｍ をもっと疎にした（10 ×10程度の）パラメータ行列とし、線形補間で、データを埋めるような対応がなされます。 

Rebonato のパラメトリックな指数関数を使うか、Piecewise Constantな行列を使うかについては、後で、Calibrationの所で、解説します。