上級編 8 クレジットデリバティブズ
8.1 CDO Tranche
8.1.4 CDO トランチの価格とデフォールトの相関との関係
Cash CDO の価格は、基本的に市場で決まりますが、デリバティブズ取引として売買された CDO Tranche(Single Tranche CDOと呼ばれています。以下“STCDO”)は、何等かのモデルを使って価格評価されます。STCDO は、Credit Default Swap ("CDS") の形で取引され、一般の CDS と同様、Premium Cash Flow と Default Cash Flow の交換になります。それぞれの Cash Flow について、その発生のタイミングと発生確率と Discount Factor を使って現在価値に換算して時価を導出しますが、その発生確率の推定に、何等かのデフォールト確率推定モデルが必要です。次のセクション以降で、そのモデルについて解説しますが、その前に、モデルのパラメータとして使われるデフォールトの相関について解説します。
CDO トランチの価格評価では、デフォールトの相関が非常に大きな影響を与えます。実際に CDO のトレーディングの現場でも、このリスクの管理は非常に難しく、欧米の大手投資銀行では、CDO トランチのトレーディング勘定の事を、Correlation Book (相関リスクを管理するトレーディングポジション)と呼んでいた程です。彼らは、サブプライムショックからリーマンショックにかけて、この相関リスクをうまく管理できず、このトレーディングで大きな損失を被りました。私自身、1990 年代の後半から 2000 年代の始めにかけて、相関のリスクがあるクレジットデリバティブズのリスク管理をした経験があります。その頃の日本では、バブル崩壊後の金融危機が深刻化しており、日系銘柄のクレジットが一斉に悪化していました。これはデリバティブズ価格に内包している相関が上昇しているのと同じ状況であり、リスク管理が非常に難しかった事を肌身で経験しました。
相関の影響は、トランチによって、方向が異なります。一般的には、相関が高いほど、エクイティ・トランチの期待損失が下がり、そのリスクを取っている Protection Seller の評価価格が改善します。逆にメザニンやシニアのトランチの期待損失が上がり、そのリスクを取っている Protection Seller の評価価格が低下します。なぜそうなるか、簡単に説明したいと思います。
< 例 >
ここで、例を用意しました。CDO の対象として、100銘柄からなるポートフォリオを想定します。仮に、その平均デフォールト確率が年率で 1% だったとします。このポートフォリオから発生する 10年の累計デフォールト確率は約 10%になるので、向こう 10年で 100銘柄中 10銘柄程度がデフォールトすると予想されます。このポートフォリオを対象とした期間5年の CDO トランチを考えてみましょう。
仮に、デフォールトの相関が0で、デフォールトの発生が、ほぼ均等に発生するケースを考えてみましょう。乱数を使ってデフォールトをシミュレーション(10年を離散的なΔtで分割し、各区間で発生したデフォールト数をカウント)すると、こんな形のデフォールト数のグラフになります。
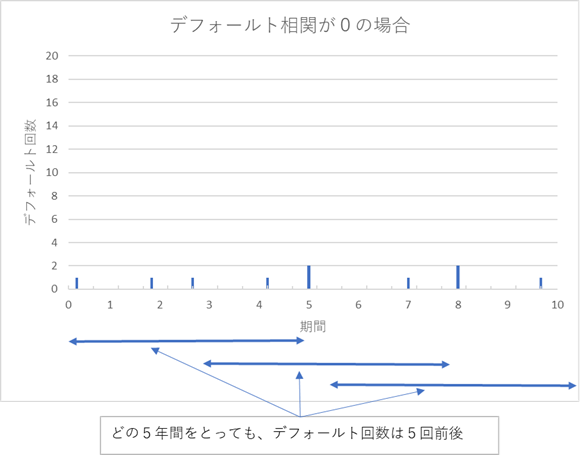
&上のグラフから分かる通り、向こう10年の内、どの5年間を取っても、その間のデフォールト回数は、おおむね5回程度になり、そこから大きくぶれません。ポートフォリオ各銘柄の債権回収率を 40% と仮定すると、5回のデフォールトから発生する損失額は、\(5×\frac{1}{100} (1-40\%)≅3\%\) 程度と見込まれ、0-3% のエクイティ・トランチは、どの期間であっても、元本をほぼ全て失う事になります。一方、メザニンやそれより優位なトランチに、損失が及ぶ可能性(期待損失)は低くなるでしょう。
では、デフォールトの相関が高い場合はどうなるでしょうか。
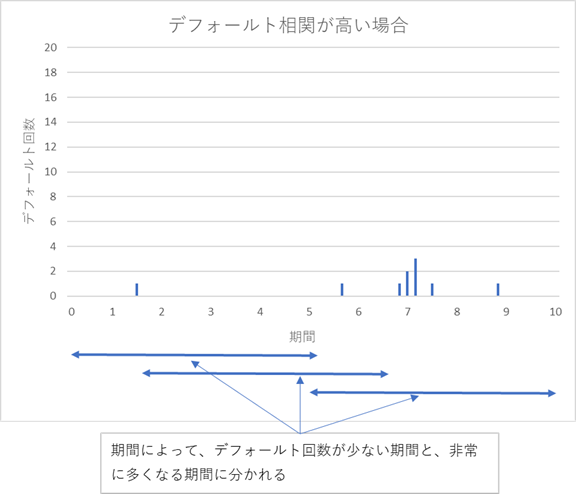
デフォールトの相関が高いと、同様のデフォールト確率の仮定(10 年間で 10 回程度のデフォールトが発生)でも、デフォールトが発生する時期が集中している期間と、まばらな期間に分かれます。すると、エクイティ・トランチのリスクを引受けた者にとって、デフォールト回数が多い時期に出くわすと、当然元本をすべて失う訳ですが、それは相関 0 の場合とあまり変わらない状況。しかしうまくいって、期間5年の間のデフォールト回数が非常に少ない期間に出くわせば、損失負担が減り元本が残る可能性が出てきます。すなわち、全体としてみれば期待損失が低下します。一方、メザニンやシニアのリスクを引受けた者にとって、運悪くデフォールトが集中する時期に出くわすと、損失額がエクイティ部分を越え、自分たちのトランチに及んでくる可能性がより高くなります。これは期待損失が上昇する事を意味します。
すなわち、相関が低いと、デフォールトのタイミングがうまく分散され、メザニンやシニアのトランチに損失が及ぶ可能性(期待損失)が低くなり、逆に、エクイティ トランチの期待損失は高くなります。 一方、相関が高くなると、デフォールトが集中する可能性が高くなり、メザニンやシニアトランチに損失が及ぶ可能性が高くなります。逆に、エクイティ・トランチは、デフォールトが疎らな時期に遭遇すれば、元本全額を失わなくてすむ可能性が出てくるので期待損失が低下します。期待損失が高くなると、Protection Seller にとっては不利になるので、プレミアムスプレッドは高くなり、期待損失が低くなると、Seller に有利なのでプレミアムスプレッドは低くなります。
過去のデフォールト事例をみても、金融危機などによりデフォールトの発生が集中する時期と、好景気が続いてデフォールトがあまり発生しない時期があるのは明白です。なので、CDO の各トランチの価格評価をする際、デフォールトの発生時期の集中(相関)をどの程度見込み、それをどうやって価格モデルに落とし込むかは、極めて重要な課題です。また、その相関の数字をどうやって求めるかも非常に難問です。デフォールトは、そもそもめったに発生するものではなく、統計的に有意なデータを集めるのが難しいからです。また、市場価格から、そこに内包されている相関の情報を取り出す方法も考えられますが、これも非常に難しく、理論的に矛盾するデータしか得られないのが実情です。
< デフォールトの相関の意味 >
デフォールトの相関という言葉を、定義を明確にせずに使ってきましたが、それを改めて明確にしたいと思います。相関係数は、複数の確率変数間の依存関係の度合いを示す係数で、一般的には、次のような関係式で求めます。(2変数の場合)
\[ ρ_{A,B}=\frac{Covar(A,B)}{\sqrt{Var(A)Var(B)}} =\frac{E(AB)-E(A)E(B)}{\sqrt{E[(A-E(A))^2 ]}\sqrt{E[(B-E(B))^2]}} \]デフォールトの相関と言う場合、この確率変数として、何を使うかが問題です。直感的に思いつくのが、デフォールトしたか否かというデジタルな情報です。デフォールトした場合を1,デフォールトしなかった場合を 0 という2項分布する確率変数を置けば、デフォールトの相関が計算できそうです。そうすると、二項分布の分岐確率は、デフォールト確率とサバイバル確率になります。この場合、適当な観測期間(例えば1年)を決め、その期間内で上の式を当てはめる事になります。上式で \(E(A),~~E(B)\) は、それぞれ\(A,~~B\) のデフォールト確率に相当し、\(E(AB)~は、A~と~B\) の両方がデフォールトする確率になります。また、分母にある、\(A~と~B\) の分散の平方根ですが、1 か 0 の2項分布の場合、\(\sqrt{(E(A)(1-E(A))E(B)(1-E(B))}\) で求まります。A と B が独立であれば、\(E(AB)=E(A)E(B)\) なので \(ρ=0\) になります。仮に 1年の期間内において、A のデフォールト確率が 1%で、B のデフォールト確率が 2%、A、B両方がデフォールトする確率が 0.025% だったとすると、下記式のようになります。
\[ ρ=\frac{0.025\%-1\% × 2\%}{\sqrt{1\%(1-1\%)×2\%(1-2\%)}} ≅ 0.26(26\%) \]この方法の問題点は、2つあって
①ひとつは、観測期間によって、相関が大きく変わってくる事です。同じデフォールト確率でも、観測期間を長くすれば相関は高くなるし、観測期間を短くすると小さくなります。なので、相関係数の決め方が恣意的になります。
②もうひとつは、\(E(A)=E(B)\) の場合に限って相関係数が 1 になり、\(E(A)=1-E(B)\) の時に限って、相関係数が-1になる事です。すなわち、相関係数を望む値にしようとすると、デフォールト確率の値に制約が出てしまうとう事です。これは、価格モデルを組み立てる上で非常に不都合です。
別の相関係数の求め方として、サバイバル時間の相関を求める方法があります。サバイバル時間とは、デフォールトが発生するまでの時間 T で、これを確率変数とみなすものです。A、B それぞれの銘柄のサバイバル時間を \(T_A,~T_B\) とすると、サバイバル時間の相関は下記式のようになります。
\[ ρ=\frac{Covar(T_A,T_B)}{\sqrt{(Var(T_A)Var(T_B)}}=\frac{E(T_A~T_B)-E(T_A)E(T_B)}{\sqrt{E[(T_A-E(T_A ))^2]} \sqrt{E[(T_B-E(T_B))^2]}} \]このサバイバル時間は、クレジットカーブが求まっていれば、シミュレーションでサンプルを求める事もできるし、\(E(T_A ),~E(T_B)\)や分散は解析的に求まります。なので相関係数 ρ、あるいは \(T_A~と~T_B\) の同時分布関数となる \(E(T_A~ T_B)\) のどちらかが与えられれば、もう一方が計算できます。
デフォールトの相関を表現する方法としてもう一つ、Robert Merton の "Structure Model"で使われている方法があります。この方法は、デフォールト(あるいはサバイバル)したか否かといったデジタルな事象を確率変数とするのではなく、デフォールトを起こす原因となる、企業の総資産価値の変動を確率変数と看做し、それの相関を取り入れる手法です。間接的ではあるものの、この相関係数を動かすことによって、デフォールトが集中する時期と、まばらな時期をうまく発生させることができます。実際に、デフォールトの相関の度合いをモデルに織り込む際は、この方法を使うのが主流になっていますので、これについては、後程、詳しく解説します。
(注:実務界でベンチマークとされている Guassian Latent Variable Model も同様の方法ですが、確率変数の意味が若干異なります。そこでは、確率変数を“企業の総資産価値”という経済的な意味を持つ値ではなく、デフォールトを起こす何かよく分からないが、正規分布する何等かの確率変数(なので“Latent Variable”)を仮定します。そして、その確率変数の相関からデフォールトの相関を表現するものです。)
< コピュラ関数 >
複数の確率変数の限界分布関数が判っている場合、それらの相関も加味した同時分布関数が、一意で定義できます。その関数をコピュラ関数と呼んでいます。コピュラ関数は、具体的な関数形を特定したものではなく、複数の確率変数の同時分布関数を総称するものです。コピュラ関数は、2001年に RiskMetrics Group の David Li氏により発表された論文(On Default Correlation)により、金融業界に紹介され、相関のリスクを持つクレジットデリバティブズの価格評価に使う為に、瞬く間に業界に広まりました。
その論文で紹介されている正規コピュラを使う方法は、その後、実務界で最も一般的に使われましたが、論文発表前に既に一部の金融機関で使われていました。それをコピュラと呼ぶ様になったのは、この論文以降です。
(注:RiskMetrics Groupは、JP Morganのリスク管理部門に所属していて、リスクの計量にValue at Riskの考え方を持ち込んだ人が、JP Morganをドロップアウトし、設立したリスク計量を専門にする会社です。JP Morganは、90年代半ばに、CreditMetricsという、ローンポートフォリオから発生する期待損失のモデルも発表していましたが、CreditMetricsが使っている手法は、正規コピュラモデルと同じものです。)