上級編 8 クレジットデリバティブズ
8.2 Gaussian Copula Model (正規コピュラモデル)
8.2.2 Structure Model
Robert Merton は、Black-Scholes-Merton モデルでノーベル賞を取った人です。そのノーベル賞の対象となったオプションモデルに関する論文は 1973年に発表されましたが、その1年後、Merton は、オプションモデルを使った、企業の負債(Corporate Debt)の価格評価モデルを発表しました(ON THE PRICING OF CORPORATE DEBT: THE RISK STRUCTURE OF INTEREST RATES - Merton - 1974 - The Journal of Finance - Wiley Online Library)。その時点で、このモデルが実務で使われる事はありませんでしたが、そこから 20~30 年後に、クレジットデリバティブズ市場が拡大していく中で、クレジット商品のリスク計測や、価格評価方法に、大きな影響を与えました。
Merton の Structure Model の概要は次の様なものです。
- まず企業の総資産価値(これを A(t) と表記します)が幾何ブラウン運動する確率過程を取ると仮定します。
- そして一定期間後、それが特定の閾値(例えば負債総額、これを D と表記)を下回ると債務超過になるので、負債の弁済能力が毀損され、デフォールトになると看做しました。
- また、その時点の企業価値と負債総額の差( A(t)-D < 0 )がデフォールト損失になると看做しました。
- すると、その負債の所有者(その企業に対する債権者)の Payoff が、企業価値を対象資産とするプットオプションの売りと同じ形持つことになります。
- そこからプットオプション価格が、その負債のリスクプレミアムに相当すると考えました。
- そして、そのリスクプレミアムを Black-Scholes-Merton のオプションモデルを使って導出しました。またそこからデフォールト確率も導出しました。
以上をもう少し詳しく説明すると、次のようになります。
(1) 企業の資産総額(バランスシートの資産総額に相当、あるいは上場企業であれば、負債+株の時価総額)を確率変数A(t)とし、それが幾何ブラウン運動すると仮定。その確率過程を下記のような確率微分方程式で記述。
\[ \begin{align}
dA(t)& =(αA(t)-C)dt + σ A(t)dW(t), \\
&但し \\
& ~~~~~ A(0) = ~ 現在の総資産価値 \\
& ~~~~~ α~:~企業が生み出す収益率の期待値(収入率) \\
& ~~~~~ C ~:~企業が支払う金利・配当率(社外流出率) \tag{8.7}
\end{align}
\]
上式のドリフト項係数 \((αA(t)-C)\) は、資産を増大させる純利益率から資産を減らす金利や配当の支払い率を差し引いた値で、要は、資産価値 \(A(t)\) を、企業活動で日々どれだけ増大(減少)させているかの期待値に相当します。
この確率過程をシミュレーションして、ランダムに \(A(t)\) の経路を生成すると、下記の例のようになります。
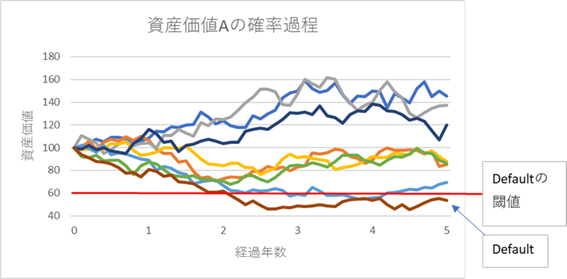
(2) 上のグラフにある通り、その確率変数 A(t) が一定の閾値(例えば負債総額。これを D と表記)を下回ると債務超過となり、負債の返済能力が毀損されデフォールトが発生すると考えます。上のグラフでは、A(t)の初期値は 100 からスタートし、閾値 D を 60 としています。すると、ランダムに生成された経路の中で、いくつかが閾値を下回り、その場合はデフォールトしたと看做されます。その時の資産価値 A と閾値 60 との際が、負債に発生する損失(Loss Given Default)と看做されます。
それをグラフにすると、下記のようになります。
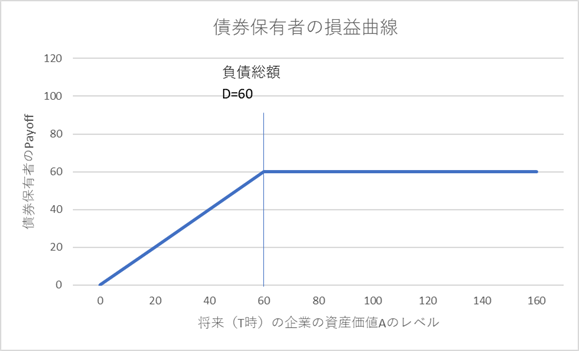
(3) 上の損益グラフは、負債の保有者(その企業に対する債権者)にとっての損益曲線(Payoff)になります。このグラフの形から分かる通り、この Payoff は、ストライクを D(=60)とする Put Option 売りと同じ形です。Merton は、そこから、この Put Option 価格が、債券保有者がデフォールトリスクを取ったリスクプレミアム(クレジットスプレッドの現在価値)に相当すると看做しました。またオプション満期時(T)において、資産価格 A(T) が閾値 D を下回っている確率をデフォールト確率と看做しました。
(4) その考え方から、デフォールトリスクのリスクプレミアムが、下記のオプション価格式(Black-Scholes-Mertonモデル)を使って計算できます。この式は、(1)で示した確率微分方程式から、一定の仮定をおいて、Black-Scholes の公式を導出したのと同じ方法で導出されます。
\[ \begin{align}
Default~& Risk ~ Premium =D e^{-rT} Φ(-d_2)-A(0)Φ(-d_1) \\
d_1 &=\frac{ \ln {A(0)/D} + (r+ \frac 1 2 σ^2)T}{σ \sqrt{T}}, \\
d_2 &=d_1-σ\sqrt{T} \tag{8.8}
\end{align}
\]
また、デフォールト確率は下記のように、標準正規分布関数を使って簡単に求める事ができます。
\[
Probability~ of~ default=P(A(T) < D)=Φ(-d_2 ) \tag{8.9}
\]
Black-Scholesのオプション価格公式に詳しい方ならお気づきだと思いますが、価格式にある \(Φ(-d_2)\) は対象資産価格がストライク価格を下回る確率になります。ここでは、A(T) が D を下回る確率、すなわち T 時にデフォールトする確率に相当します。なので \(1-Φ(-d_2)=Φ(d_2)\) がサバイバル確率になります。
いかがでしょう。Merton の Structure Model は、企業が債務超過になってデフォールトを起こすという経済現象とオプションモデルを組み合わせたという点が慧眼です。しかし、総資産価値A(t)の観測が簡単ではない事や、他にもかなり極端な仮定を置いている事などから、実務の場でこれがそのまま使われる事は、殆どありませんでした。
しかし後に Vasicek が、このモデルの考え方を応用する形で、複数の企業に対するローンポートフォリオから発生する損失モデルを提起しました。それが、後々の Gaussian Copula Model の原型になります。では、その Vasicek の Loan portfolio model の解説に移ります。